Klassendiagramme
Klassendiagramme modellieren die statischen strukturellen Beziehungen zwischen den Komponenten eines Systems.
Klassendiagramme sind der Hauptbaustein der objektorientierten Modellierung.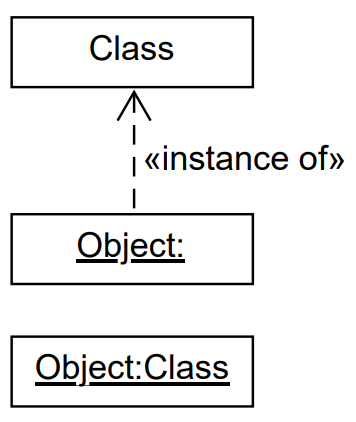 
Scopes und Multiplizität
Gültigkeitsbereich (scope):
Pfadnamen können in Klassendiagrammen verwendet werden, um den Gültigkeitsbereich (scope) der Klasse zu identifizieren,
z.B. org::openoffice::SpellChecker
Multiplizität von Klassen:
In der oberen rechten Ecke einer Klasse kann die Multiplizität (d.h. Anzahl der Instanzen) einer Klasse sein:
Keine Zahl in der oberen rechten Ecke: mehr als eine Instanz einer Klasse möglich
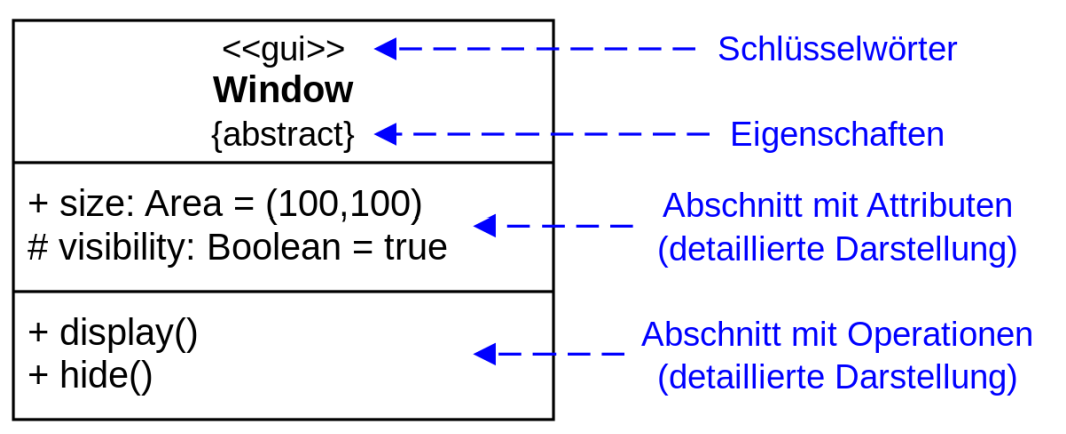
Klassenattribute stellen die Eigenschaften (properties) einer Klasse dar.
| Sichtbarkeit von Attributen + öffentlich: Unbeschränkter Zugriff # geschützt: Zugriff von Klasse sowie von Unterklassen − privat: Nur die Klasse selbst kann das Attribut sehen ~ paketsichtbar: Innerhalb des Pakets sichtbar |
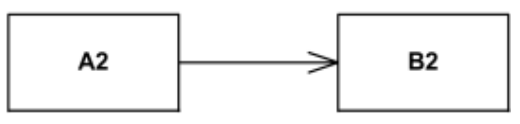
Arten von Beziehungen Dependency: Abhängigkeit zwischen zwei Klassen Assoziation: lies “hat ein” Aggregation: Spezieller Typ der Assoziation, lies “besitzt ein” Komposition: Stärkste Beziehung zwischen Klassen, lies “besteht aus” Generalisierung: Vererbungsbeziehung, lies “ist ein” Realisierung: Implementierung einer Schnittstelle |
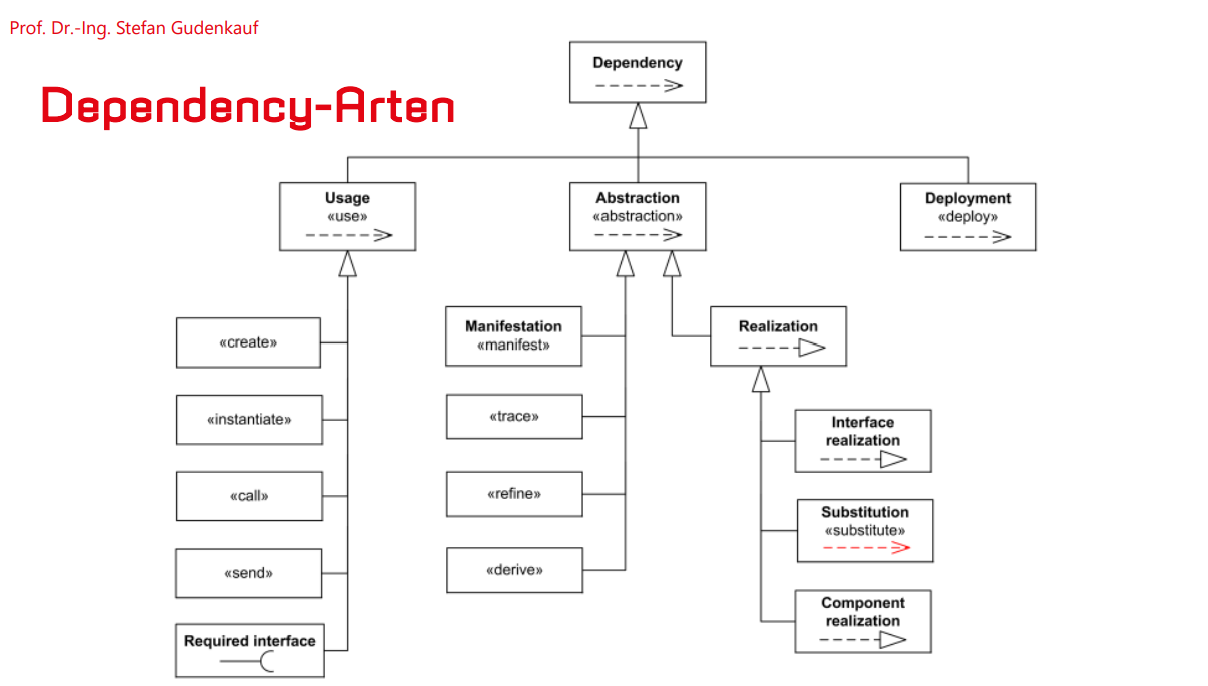
Nutzungsabhängigkeit – Angabe, dass ein Element ein anderes Element oder eine Menge von Elementen für seine Implementierung benötigt.
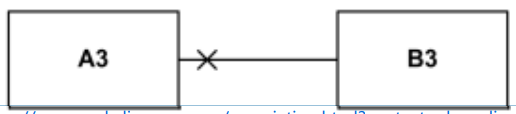
Assoziation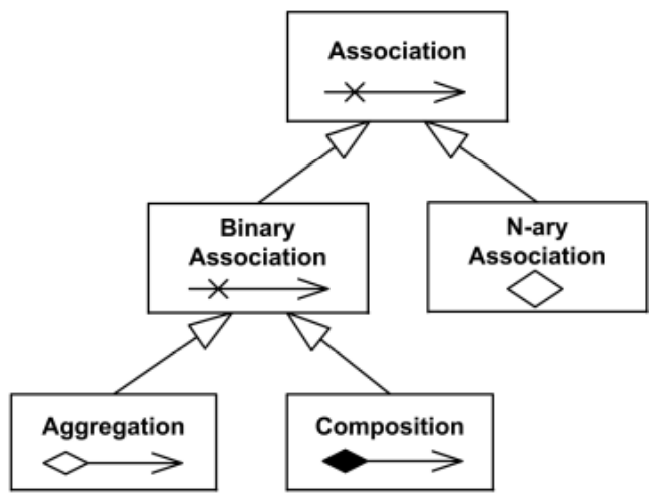 
– Angabe, dass Typinstanzen miteinander in Verbindung stehen oder logisch bzw. physisch miteinander zu einer Aggregation kombiniert werden können. z.B: Wrote:
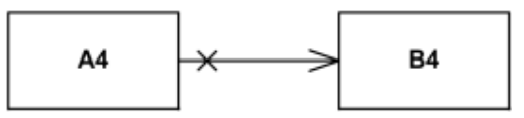
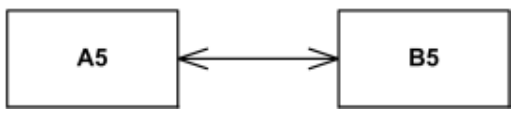
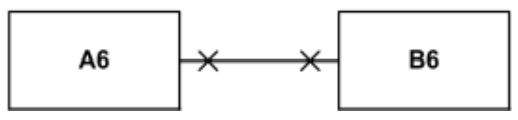
Navigierbarkeit von Assoziationen
|
Beide Enden der Assoziation haben eine nicht spezifizierte Navigierbarkeit: |
A2 hat nicht spezifizierte Navigierbarkeit, während B2 von A2 aus navigierbar ist:
|
A3 ist von B3 nicht navigierbar, wenn B3 nicht spezifizierte Navigierbarkeit hat:
|
|
A4 ist von B4 aus nicht navigierbar, während B4 von A4 navigierbar ist:
|
A5 ist von B5 aus navigierbar und umgekehrt:
|
A6 ist von B6 aus nicht navigierbar und umgekehrt
|
Stelligkeit von Assoziationen:
Binäre Assoziationen: verbindet genau zwei Typen bzw. Klassen.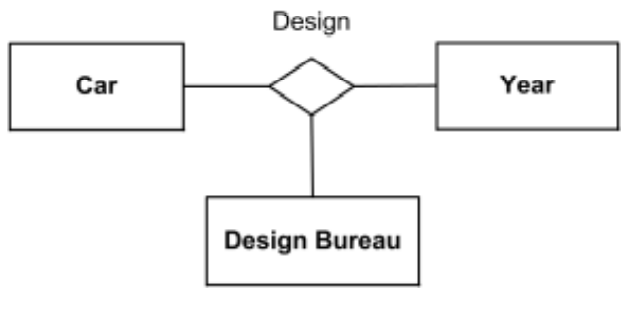
n-äre Assoziationen mit mehr als zwei Assoziationsenden
Multiplizität (Kardinalität) - Definition Anzahl maximal Elemente durch inklusives Intervall nichtnegativer Ganzzahlen
| Multiplizität | Option | Bedeutung |
| 0..0 | 0 | Keine Instanzen (leere Menge) |
| 0..1 | Keine oder eine Instanz | |
| 1..1 | 1 | Genau eine Instanz |
| 0..* | * | Null oder mehr Instanzen |
| 1..* | Mindestens eine Instanz | |
| 5..5 | 5 | Genau fünf Instanzen |
| m..n |
Mindestens , aber nicht mehr als Instanzen |
Beispiel:
Jeder Professor kann (als author) ein oder mehrere Bücher schreiben (kann sein lassen): 0..*
Jedes Buch (als textbook) ist von mindestens einem Professor geschrieben: 1..*
Multiplizität
Ordnung ( ordered oder unordered )
Einzigartigkeit der Elemente ( unique oder nonunique )
Standardgemäß sind Elemente eines Intervalls unordered und unique
Aggregation - Eine binäre Assoziation, die eine Teile-Ganzes Beziehung darstellt.
Asymmetrisch: nur ein Ende der Assoziation kann eine Aggregation sein
Transitiv: Aggregationsverknüpfungen sollten gerichteten, azyklischen Graph bilden, so dass keine Instanz Teil seiner selbst ist
Unabhängig: Wenn übergeordnete Instanzen gelöscht werden, können die untergeordneten Teile-Instanzen weiterbestehen
(shared) Aggregation
Ein Dreieck hat drei einzigartige Liniensegmente, die als Seiten bezeichent werden.
Die Liniensegmente sind von Dreieck (Triangle) aus navigierbar.
Die Komposition
Komposition - Eine binäre Assoziation, die eine Teile-GanzesBeziehung darstellt und es gilt:
1. Ein Teil kann zu einem Zeitpunkt höchstens in einem Ganzen (engl. whole, composite) enthalten sein. 
2. Wenn ein Ganzes gelöscht wird, werden alle seine Teile mit diesem gelöscht.
Die Generalisierung
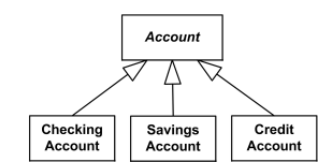
Generalisierung - Eine binäre taxonomische Beziehung zwischen einem allgemeineren Typ
Realisierung
Realisierung odellelementen, von denen eine die Spezifikation und die andere deren Implementierung (Kunde) darstellt.
Spezielle Realisierung zwischen einem Klasse und einer Schnittstelle. 
Operation (engl. operation) -- Verhaltensmerkmal einer Schnittstelle, eines Datentyps oder Klasse
Datentyp -- Typ, dessen Instanzen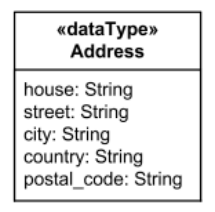
nur durch ihren Wert bestimmt sind
Aufzählung ( enumeration) -- Datentyp, dessen Werte benutzerdefinierte Literale sind
No Comments